In “Operations Research in Practice (Part 2): Generic Problems”, we discussed the second step of OR in pratice. Once an operations researcher successfully converts the business problem into an OR generic problem, the next step is to formulate the generic problem into a mathematical model. In this step we will describe the generic problem using some modelling paradigms.
A modeling paradigm is a set of concepts, including theories, rules, and standards for representing real-world problems using mathematical languages. The most known and used modeling paradigms in OR include linear, integer, mixed-integer, and convex programming.

These modeling paradigms is powerful tools to represent optimization problems, and the word “programming” above refers to “optimization”. In the simplest case of an optimization problem we look for the largest value (maximization problem) or the smallest value (minimazation problem) that a function can take. An optimization problem consists of objective function and a set of constraints. For example, if we want to minimize the cost of production the constraints could be related to time, workers, and materials.
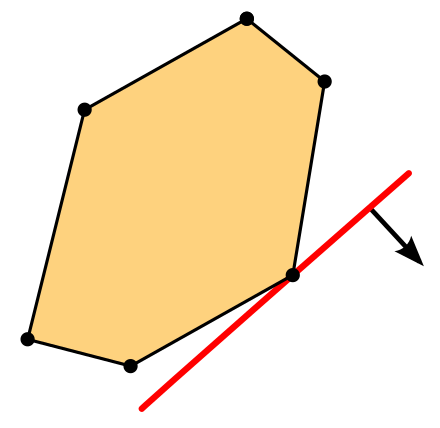
The problem we have in hand will be formulated using one of the modeling paradigms mentioned above. Which one(s) to use depends on the nature of the problem. Linear programming is used when we have a linear function as the objective function, i.e. we want to maximize or minimize linear function, given a set of linear constraints. In linear programming the decision variables, the unknown variables that we need to pick to maximize or minimize the objective function, should be real numbers. Below is an example of graphical representation of a simple linear program with two variables and six inequalities.

When the decision variables are integers, we use integer programming to represent the problem. When some of decision variables are integers and some of them are real numbers, mixed-integer programming is used. The main reasons for using integer variables are the following.
- The integer variables represent quantities that can only be integer. e.g. it is not possible to produce 3.7 cars.
- The integer variables represent decisions, e.g. whether to produce at a certain time, and thus should only take on the value 0 or 1.
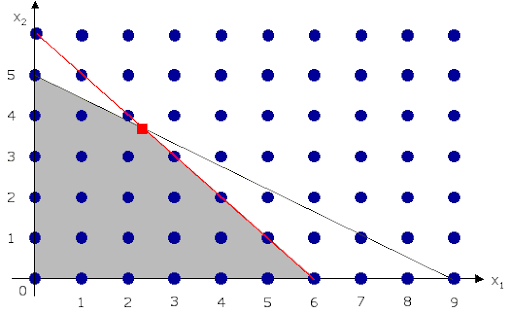
These considerations occur frequently in practice and are useful in many applications including production planning, scheduling, and telecommunications networks. In the illustration below, while a linear program can take on any value in the grey area, an integer program solution can only be one of the blue dots.

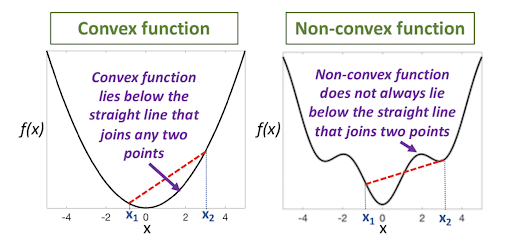
Another widely used modeling paradigm is convex programming. A convex optimization problem is a problem where we minimized a convex function and all of the constraints are convex functions. Linear functions are convex, so linear programming problems are convex problems. Solving convex optimization is guaranteed to achieve the global minimum. The figures below illustrate the definition of convex and non-convex functions.

Once we formulate the problem into an optimization problem using a certain modeling paradigm, the next step is to solve it. There are several popular algorithms that have been developed to solve linear, integer, and convex optimization problems. We’ll discuss the next step of OR in practice, which is solving the optimization problems using some algorithms, in the next article. In the meantime, contact us to explore our service related to Operations Research and get further information by sending an email to [email protected].



